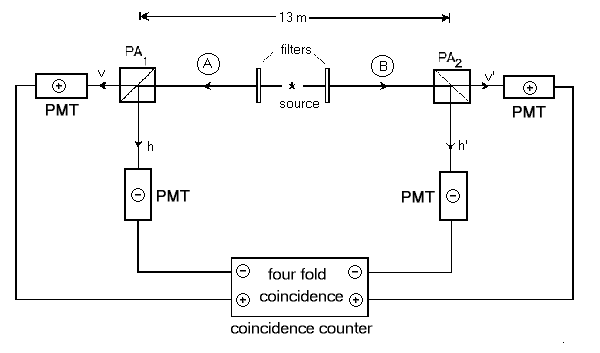
From a Quantum Mechanical point of view, what happens to photons in the Aspect experiment?1   To begin with, we know that the light leaving the source will be circularly polarized in opposite directions but, since the detectors are facing in opposite directions, the two detectors should see the same direction of circular polarization. The wavefunction which spreads throughout this experiment will be in a superposition of both left- and right-circularly polarized light. As this wavefunction reaches the polarization filters at each end of the experiment (PA1 and PA2), it will split with part of the wavefunction heading to each of the four detectors. Notice here that one single wavefunction connects all four detectors. It is not possible to separate out what is going on at each of the detectors because it is not possible to separate out the left- and right-circular polarization states. Because of the symmetric nature of bosons (and hence, photons), we can write the wavefunction for the creation of the two circularly polarized photons as: | Y > = 0.707 ( |YAL>|YBL> + |YAR>|YBR> ) (1) where the superscript refers to which arm of the experiment the ket describes and the subscript denotes the polarization of the ket as either left-circularly polarized (L) or right-circularly polarized (R). Now, let "+" signify that the PMT tube along the path of vertically polarized photons registered the photon and let a "-" signify that the PMT tube along the other path registered the photon. These values are the same ones which are sent to the coincidence counter and are the same as the labels in the figure below. This choice of +1 and -1 means that the eigenvalues for the detectors are +1 fora vertically polarized photon and a -1 for a horizontally polarized photon. If one wants to write down the wavefunction describing an event where the photon along path A registers as a vertically polarized photon relative to PA1 (denoted as the unprimed frame) and the photon along path B registers as a vertically polarized photon relative to PA2 (denoted as the primed frame), then one can write this wavefunction as: | Y ++> = |YAv>|YBv' > where v stands for linear polarization aligned with the axis of the filter PA1 and v' stands for linear polarization aligned with the axis of the filter PA2. Similarly, we find that the other possible resulting wavefunctions are: | Y +-> = |YAv>|YBh'> | Y -+> = |YAh>|YBv'> | Y --> = |YAh>|YBh'> (2) Since these four kets represent the only possible outcomes of this experiment, they must spand the result space and thus they form a complete basis set. Recall now that, given a wavefunction in one basis, we can always expand it into any other complete basis. Thus, our |Y> from equation 1 becomes: |Y++ > < Y++|Y>   +   |Y+- > < Y+-|Y>   +   |Y-+ > < Y-+|Y>   +   |Y-- > < Y--|Y> (3) We now ask the question, what is the probability that both detectors will register a "+"? In equation 3, the wavefunction which represents this outcome is |Y++> and the square of its coefficient will represent the probability of it occuring. So, the probability of getting two "+" results is just |< Y++|Y>|2. All that is left now is to determine what all the coefficients in equation 3 are. We can take advantage of the fact that the kets in equation 2 are all orthonormal. So, for example, < Y++ | Y++> = 1, but < Y++ | Y+-> = 0. As a general result, if we let "i" and "j" each stand for either "+" or "-", then using equations 1, 2, and 3, we find that: < Yij|Y> = .707(   < YAi|YAL> < YBj|YBL>  +   < YAi|YAR> < YBj|YBR>   ) (4) All of these matrix elements relate a linear polarization state to a circular polarization state. These matrix elements work out to be:(click here for derivation) 2 |Yv> |Yh> |Yv'> |Yh'> |YL> |YR> < Yv| 1 0 cos(t) sin(t) 0.707 0.707 < Yh| 0 1 -sin(t) cos(t) 0.707i -0.707i < Yv'| cos(t) -sin(t) 1 0 .707 e-it 0.707 eit < Yh'| sin(t) cos(t) 0 1 .707 ie-it -0.707 ieit < YL| 0.707 -0.707 i 0.707 eit -0.707 ieit 1 0 < YR| 0.707 0.707 i .707 e-it .707 ie-it 0 1 where t is the angle between the orientation of PA1 and PA2, and i is the square-root of -1. Notice that, if we are just transforming linear polarization vectors from the primed frame to the unprimed frame, the project amplitudes are those derivable from planar geometry. In addition, all the projections have been orthonormalized with an arbitrary, but consistent, phase factor. Using the above table and equation 4, we find that: < Y++|Y > = (.5)(.707)(eit+e-it)=0.707 cos(t) < Y+-|Y > = (-.5i)(.707)(eit-e-it)=0.707 sin(t) < Y-+|Y > = (-.5i)(.707)(eit-e-it)=0.707 sin(t) < Y--|Y > = (-.5)(.707)(eit+e-it)= -0.707 cos(t) (5) We can substitute these expressions back into equation 3 and show that: |Y > = 0.707 ( |Y++>cos(t)  +  |Y+->sin(t)  +  |Y-+>sin(t)  -  |Y-->cos(t)  ) (6) The quantity which we are interested in is the expectation value for the experimental setup. This should be: E(a,b)   =   P++(a,b)RAvRBv'   +   P+-(a,b)RAvRBh'   +   P-+(a,b)RAhRBv'   +   P--(a,b)RAhRBh' where Pij(a,b) means that detector A, with orientation a, detected state i (either "+" or "-") and detector B, with orientation b, detected state j; and where RAv stands for the expectation value corresponding to "arm" A detecting a photon whose polarization is aligned with the axis of PA1. Recall that we already know what the expectation values, R, are - they are ± 1! Therefore, E(a,b) = P++(a,b) - P++(a,b) - P++(a,b) + P++(a,b) (7) The Pij's are merely the matrix elements listed in equation 5 squared (Pij = |< Yij|Y> |2 ). Finally, the expectation value, according to Quantum Mechanics, for this experiment, is: E(a,b) = .5 ( cos2(t) - sin2(t) - sin2(t) + cos2(t) ) = cos2(t) - sin2 (t) = cos(2t) where "t" is the angle between a (the orientation of PA1) and b (the orientation of PA2).

²ibid. chapter 2.5.