

|
|
| |
|
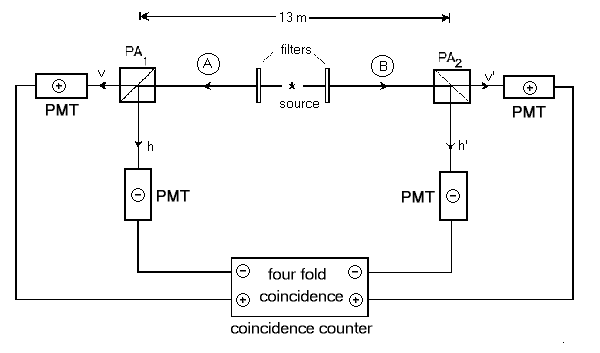
Shown below is a diagram of the Aspect experimental setup.
1 The Hidden
Variable Theory says that nature is deterministic and, despite
what may be predicted by Quantum Mechanics, particles always have a
definite position. What happens to the photons which are produced
in this experiment? When a blue photon is produced at the source, if
it travels to the left down path A, then it will be blocked by
the filter along that path. If, on the other hand, it travels down
path B, it will pass through the filter and travel to the polarization
analyser PA2.
The polarization of the photons produced by the source are oriented randomly. Using quantum mechanics alone, we cannot make any predictions about this polarization. But, there are aspects of the theory (hidden variables) which ensure that the photon must have a definite value of polarization. So, half the time our blue photon will pass through the filter and the other half of the time it will be deflected by the filter. It is important to note two things at this point. First, the photon is EITHER deflected by the filter OR it passes through the filter; one or the other, never both. Secondly, the direction which the photon takes depends ONLY on its polarization - it does not depend on any other photon in this experiment nor does it depend on the orientation of the filter PA1. These two details are the separability and locality conditions required in John Bell's solution to the EPR paradox. Finally, the photons travel down to the photo-multiplier tubes and are registered by the coincidence counter. |
|
|
| |
If we run this experiment, what do we expect to find?
2 First of all,
the expectation value for a particular measurement of this system,
with specific values of a and b, is given
by the formula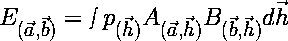 , ,where p(h) is the probability density function for the unknown hidden variables h. Now, if we run this same experiment again but we change the orintatin of PA2 from b to d, the expectation value for this run will be the same as above with b replaced by d. If we subtract the expectation values for the two runs, we have equation 1: |
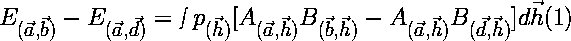
|
|
| |
| Since the absolute value of A(a,h) must be less than or equal to 1, equation 1 becomes: |
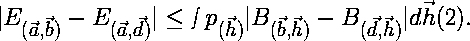
|
|
| |
| By substituting c for a in equation 2 and changing the minus sign to a plus sign, one can see that: |
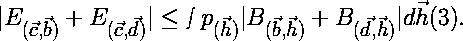
|
|
| |
|
Now, if we add equations 2 and 3 together, we get: |
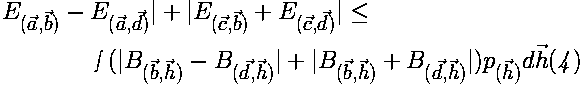
|
|
| |
|
This particular combination of four expectation values given on the
left-hand side of equation 4 is denoted as S.
Since the absolute value of both B(b,h)
and B(d,h) are less than or equal to
1, we can attempt to find an upper limit for the integral on the right
hand side of equation 4. This can be done by finding the maximum
value for equation 5: 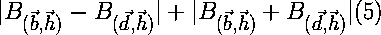 There are four possibilities:
Since the maximum value for equation 5 in every case is 2, then equation 5 must always be less than or equal to 2. So, the right side of equation 4 becomes: |
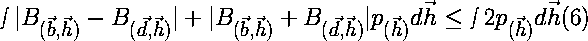
|
|
| |
| Recall now that p(h) is a normalized probability density. So, the integral of p(h) over all h must equal 1. Thus, you can see that in any experiment of this type, S (where S is the left-hand side of equation 4) is constrained to be less than or equal to 2. |