Experiment Results

In this experiment, the important quantity to measure is not merely the average result for one set of detector settings, but a very specific combination.¹ As we discussed previously in the section which describes the experimental setup, the important quantity is S = | E_(a,b) - E_(a,d) | + | E_(c,b) E_(c,d) |. Now, according to the analysis of Hidden Variable Theories, S must be less than or equal to 2.

Quantum Mechanics, on the other hand, makes quite a different prediction. If PA₁ is set to detect linear polarization along a direction given by a and PA₂ is set to detect linear polarization along a direction given by b then the expectation value according to Quantum Mechanics is E_{(a, b)} = cos(2t), where t is the angle between vectors a and b. Using this result, we can predict a value for S which is greater than 2. For example:

Angle of PA₁	Angle of PA₂	Angle t	Expectation
0° (a) 0° (a) 45° (c) 45° (c)	22.5° (b) 67.5° (d) 22.5° (b) 67.5° (d)	22.5° 67.5° -22.5° 22.5°	0.707 -0.707 0.707 0.707

Using these values, Quantum Mechanics would predict S to be | 0.707 - (-0.707) | + | 0.707 + 0.707 | = 2.828. The predictions of a hidden variable theory were that S must be less than or equal to 2, Quantum Mechanics predicts that S should be 2.828. Thus, this experimental setup, done with the four detector settings shown in the table above, can determine whether or not the hidden variable approach to solving the EPR paradox is correct.

Before we present the results of the experiment, there are a few more technical aspects which we must discuss. The setup is not perfect. For example, the detectors only can see a finite solid angle and the polarization filters are not perfect. We can adjust the expectation values predicted by Quantum Mechanics by the following factor:

F [ (T^v_A - T^h_A) (T^v_B - T^h_B) ] / [ (T^v_A + T^h_A) (T^v_B + T^h_B) ]

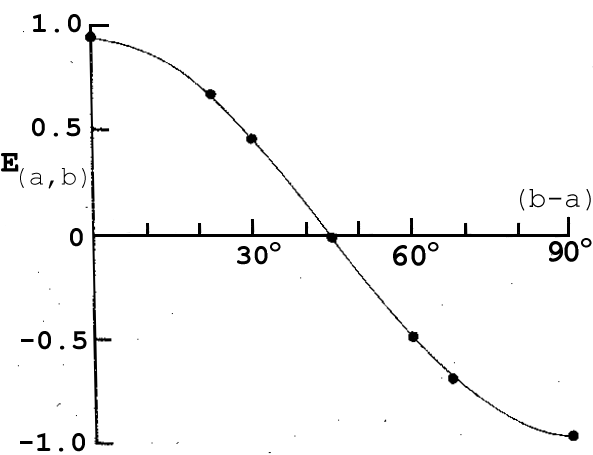
where F stands for the finite solid angle of the detectors, T^v_A is the transmission coefficient for vertically polarized light passing through the A filter, T^h_A is the transmission coefficent for horizontally polarized light passing through the A filter, and so on. For this experiment, the equipment used had the following values:
F = .984 (7.83% of a sphere), T^v_A = .950 , T^h_A = .007 , T^v_B = .930 , T^h_B = .007. Therefore, the predicted expectation values need to be multiplied by 0.955. This changes the cosine wave predicted by Quantum Mechanics for the expectation value to 0.955 cos(2t). This will change S from 2.828 to 2.70.

All that is left is to report the data. From the experiment, S was measured to be 2.697 ± 0.015. This value is clearly in violation of the hidden variable prediction and corresponds almost exactly to the quantum mechanical description! In addition to this result, a plot of the experimental expectation values verses the angle between the two detector orientations is given below.² The line in the graph is not a best fit to the curve, it is a plot of 0.955 cos(2t), the Quantum Mechanically predicted expectation value. Quantum Mechanics has predicted not only the correct value for S but also the correct dependance of the expectation value on the detector angles.

Return to the main page
Description of the Experiment
Predictions of the Hidden Variable Theory
Predictions of Quantum Mechanics
What now?

¹ The Meaning of Quantum Theory. Jim Baggott. Oxford University Press, Oxford 1992, chapter 2, 4, appendix B.
² The Meaning of Quantum Theory, figure 4.10, page 144.

Please send comments and questions to:
eric@roxanne.org