Projection Amplitudes

going from linear to circularly polarized light

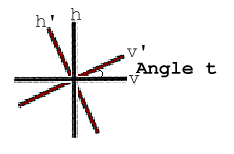
In this section, we would like to derive the transformations needed when we want to convert one type of polarization into another basis. Lets assume that we have two coordinate systems, one primed and one unprimed, such that the angle between the systems is "t". In addition to merely changing the coordinate system of a polarization vector, we will also want to be able to switch from linear polarization to circular polarization.

To start with, because a vector projected onto itself has a magnitude of 1 and a vector projected onto another orthogonal vector is zero, we have:

| < Y_v|Y_v> |² = | < Y_v'|Y_v'> |² = | < Y_h|Y_h> |² = | < Y_h'|Y_h'> |² = 1
| < Y_v|Y_h> |² = | < Y_v'|Y_h'> |² = | < Y_v|Y_h'> |² = | < Y_h|Y_v'> |² = 0 (1)
If we have two coordinate systems as in the figure above, then we can see that:

|Y_v > = |Y_v'>cos(t) + |Y_h'>sin(t)
|Y_h > = |Y_h'>cos(t) - |Y_v'>sin(t) (2)
By using the above relationships and by multiplying equation 2 with the appropriate bra's, one can derive the follwing equations:
< Y_v'|Y_v> = < Y_v|Y_v'> = cos(t)
< Y_v'|Y_h> = < Y_h|Y_v'> = -sin(t)
< Y_h'|Y_v> = < Y_v|Y_h'> = sin(t)
< Y_h'|Y_h> = < Y_h|Y_h'> = cos(t) (3)

Now, we can choose to expand the v' ket in terms of another basis by means of the expansion theorem. If we expand onto the circular polarization basis we get:

|Y_v'> = |Y_L>< Y_L|Y_v'> + |Y_R>< Y_R|Y_v'>
and
< Y_v|Y_v'> = < Y_v|Y_L< Y_L|Y_v'> + < Y_v|Y_R< Y_R|Y_v'> (4)

We know that linearly polarized light is made up of equal parts of left- and right-circularly polarized light. So, |< Y_v|Y_L>| = 0.707, as well as the elements relating v and R, h and L, and h and R. From the relationshps in equation 3, one can see that equation 4 must equal cos(t). The only way this is possible is if the projection amplitudes are complex.
At this point, we can choose any solutions for the above projection amplitudes as long as they collectively satisfy the above equation. Therefore, we can write each factor as follows:

< Y_v|Y_L> = 0.707
< Y_v|Y_R> = 0.707
< Y_L|Y_v'> = 0.707 e^it
< Y_R|Y_v'> = 0.707 e^-it (5)

We can now follow a similar procedure to find two more coefficients by replacing v' in equation 4 with h':
< Y_v|Y_h'> = < Y_v|Y_L< Y_L|Y_h'> + < Y_v|Y_R< Y_R|Y_h'> (6)

We recognise that, from equation 5, < Y_v|Y_L> = < Y_v|Y_R = 0.707. Also, since < Y_v|Y_h' is sin(t), we find that (again using the same phase convention) that:
< Y_L|Y_h'> = -0.707ie^it
< Y_R|Y_h'> = 0.707ie^-it (7)

The last two elements can again be found by the same procedure.

< Y_L|Y_h> = -0.707i
< Y_R|Y_h'> = 0.707i (7)

Now, we can use these elements to build a transformation table, noting that the transpose of each entry is merely its complex conjugate. The table is:

|Y_v> |Y_h> |Y_v'> |Y_h'> |Y_L> |Y_R>

< Y_v| 1 0 cos(t) sin(t) 0.707 0.707

< Y_h| 0 1 -sin(t) cos(t) 0.707i -0.707i

< Y_v'| cos(t) -sin(t) 1 0 .707 e^-it 0.707 e^it

< Y_h'| sin(t) cos(t) 0 1 .707 ie^-it -0.707 ie^it

< Y_L| 0.707 -0.707 i 0.707 e^it -0.707 ie^it 1 0

< Y_R| 0.707 0.707 i .707 e^-it .707 ie^-it 0 1

Return to Quantum Mechanics Derivation

¹ The Meaning of Quantum Theory. Jim Baggott. Oxford University Press, Oxford, 1992, chapter 2.5.

Please send comments and questions to:
eric@roxanne.org